Série de Fourier - de Wolfram MathWorld
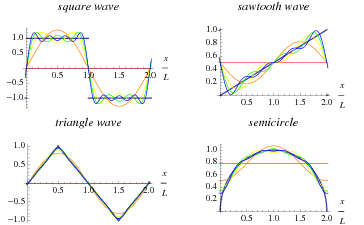
Une série de Fourier est une extension d'une fonction périodique en termes d'une somme infinie de sinus et cosinus. série de Fourier utilisent des relations d'orthogonalité des fonctions sinus et cosinus. Le calcul et l'étude des séries de Fourier est connu comme l'analyse harmonique et est extrêmement utile comme moyen de briser une fonction périodique arbitraire dans un ensemble de termes simples qui peuvent être branché, résolu individuellement, puis recombiner pour obtenir la solution au problème d'origine ou d'une approximation à ce que la précision est souhaitée ou pratique. Des exemples d'approximations successives à l'aide de fonctions communes séries de Fourier sont illustrés ci-dessus.
En particulier, étant donné que le principe de superposition est valable pour des solutions d'une équation différentielle ordinaire linéaire homogène. si une telle équation peut être résolue dans le cas d'une seule sinusoïde, la solution pour une fonction arbitraire est immédiatement disponible en exprimant la fonction originale en une série de Fourier et ensuite de brancher la solution pour chaque composante sinusoïdale. Dans certains cas particuliers où la série de Fourier peut se résumer sous forme fermée, cette technique peut même donner des solutions analytiques.
Tout ensemble de fonctions qui forment un système orthogonal complet ont une série de Fourier généralisée correspondant analogue à la série de Fourier. Par exemple, en utilisant orthogonalité des racines d'une fonction de Bessel du premier type donne une série de Fourier-Bessel dite.
Le calcul de la série de Fourier (habituel) est basée sur les identités intégrales
Utilisation de la méthode pour une série de Fourier généralisée. on obtient la série de Fourier habituelle impliquant sinus et cosinus en prenant et. Étant donné que ces fonctions forment un système orthogonal complet sur la série de Fourier d'une fonction est donnée par
et, 2, 3. On notera que le coefficient du terme constant a été écrit dans une forme particulière par rapport à la forme générale d'une série de Fourier généralisée afin de préserver la symétrie avec les définitions des termes et.
Une série de Fourier converge vers la fonction (égale à la fonction d'origine à des points de continuité ou à la moyenne des deux limites aux points de discontinuité)
si la fonction satisfait que l'on appelle les conditions de Dirichlet. Le test de Dini donne une condition pour la convergence des séries de Fourier.
En conséquence, près des points de discontinuité, une « Ringing » connu comme le phénomène de Gibbs. illustré ci-dessus, peut se produire.
Pour une fonction périodique sur un intervalle au lieu de, un simple changement des variables peut être utilisé pour transformer l'intervalle d'intégration de à. Laisser