Transformée de Fourier pour les nuls - Mathématiques Stack échange
Les anciens Grecs avaient une théorie que le soleil, la lune et les planètes se déplacent autour de la Terre dans les milieux. Cela a été rapidement démontré faux. Le problème est que si vous regardez les planètes soigneusement, parfois ils se déplacent en arrière dans le ciel. Alors Ptolémée est venu avec une idée nouvelle - les planètes se déplacent dans un grand cercle, mais se déplacent alors autour d'un petit cercle en même temps. Pensez à tenir un long bâton et tourner autour, et en même temps sur la fin du bâton, il y a une roue qui est en rotation. La planète se déplace comme un point sur le bord de la roue.
Eh bien, une fois qu'ils ont commencé à regarder de très près, ils ont réalisé que même cela ne fonctionne pas, alors ils ont mis des cercles sur des cercles sur des cercles.
Finalement, ils avaient une carte du système solaire qui ressemblait à ceci:
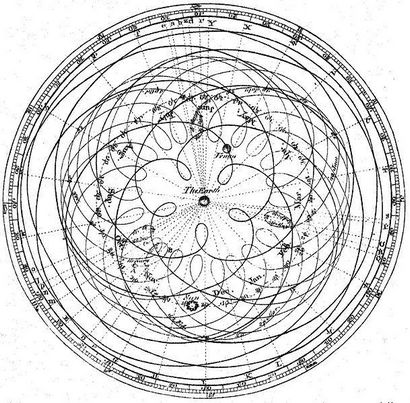
Cette idée des « épicycles » se révèle être une mauvaise théorie. Une raison pour laquelle il est mauvais est que nous savons maintenant que les planètes en orbite dans des ellipses autour du soleil. (Les points de suspension ne sont pas parfaits parce qu'ils sont perturbés par l'influence d'autres organismes qui gravitent, et par des effets relativistes.)
Mais il est faux pour une raison encore pire que cela, comme illustré dans cette merveilleuse vidéo de youtube.
Dans la vidéo, en ajoutant des cercles assez, ils ont fait une planète tracent le visage d'Homer Simpson. Il se trouve que nous pouvons faire une orbite tout en ajoutant des cercles assez, aussi longtemps que nous obtenons de faire varier leur taille et leur vitesse.
Ainsi, la théorie de epicycle des orbites planétaires est un mauvais pas parce qu'il est mauvais, mais parce qu'il ne dit rien du tout sur les orbites. Prétendant « planètes se déplacent dans épicycles » est mathématiquement équivalent à dire « planètes se déplacent en deux dimensions ». Eh bien, ce n'est pas rien dire, mais ce n'est pas dire grand-chose, non plus!
Une façon mathématique simple pour représenter « se déplacer dans un cercle » est-à-dire que les positions dans un plan sont représentés par des nombres complexes, donc un point mobile dans le plan est représenté par une fonction complexe de temps. Dans ce cas, le déplacement sur un cercle de rayon $ R $ et de la fréquence angulaire $ \ omega $ est représentée par la position
Si vous vous déplacez sur deux cercles, l'un à la fin de l'autre, votre position est
On peut alors imaginer trois, quatre ou infiniment beaucoup de ces cercles étant ajouté. Si nous permettons aux cercles d'avoir toutes les fréquences angulaires possibles, nous pouvons maintenant écrire
La fonction R $ (\ omega) $ est la transformée de Fourier de $ z (t) $. Si vous commencez par tracer une voie en fonction du temps que vous voulez grâce à deux dimensions, votre chemin peut être parfaitement imitée par une infinité de cercles de fréquences différentes, toutes additionnées, et les rayons de ces cercles est la transformée de Fourier de votre chemin. Avertissement: nous devons permettre aux cercles d'avoir des rayons complexes. Ce n'est pas étrange, cependant. C'est la même chose que de dire les cercles ont des rayons réels, mais ils n'ont pas tous commencer au même endroit. Au temps zéro, vous pouvez commencer à aussi loin que vous voulez autour de chaque cercle.
Si votre chemin se referme sur elle-même, comme dans la vidéo, la transformée de Fourier se révèle simplifier une série de Fourier. La plupart des fréquences ne sont plus nécessaires, et nous pouvons écrire
où $ \ omega_0 $ est la fréquence angulaire associée à la chose toute répétition - la fréquence du plus lent cercle. Les cercles que nous avons besoin sont le plus lent cercle, puis une deux fois plus vite que cela, alors un trois fois plus vite que le plus lent, etc. Il y a encore des cercles infiniment beaucoup si vous voulez reproduire un chemin répétitif parfaitement, mais ils sont comptablement infini maintenant. Si vous prenez le vingt et unième ou si et laissez tomber le reste, vous devriez vous rapprocher de votre réponse souhaitée. De cette façon, vous pouvez utiliser l'analyse de Fourier pour créer votre propre vidéo épicycles de votre personnage de dessin animé préféré.
C'est ce que l'analyse de Fourier dit. Les questions qui restent sont à le faire, ce qu'il est, et pourquoi cela fonctionne. Je pense que je vais surtout laisser les seuls. Comment faire - comment trouver $ R (\ omega) $ z donné $ (t) $ se trouve dans un traitement d'introduction, et est assez intuitive si vous comprenez orthogonalité. Pourquoi cela fonctionne est une question assez profonde. Il est une conséquence du théorème spectral.
Il m'a fallu un certain temps pour comprendre ce que l'on entend exactement par transformée de Fourier, car il peut se référer à différents algorithmes, les opérations et les résultats. Bien que je suis tout à fait nouveau dans ce sujet, je vais essayer de donner un bref aperçu, mais je l'espère intuitive sur ce que je suis venu avec (ne hésitez pas à me corriger):
Disons que vous avez une fonction $ f (t) $ qui associe une valeur de temps $ t $ à une valeur $ f (t) $.
Maintenant, nous allons essayer de rapprocher $ f $ la somme des oscillations harmoniques simples, à savoir des ondes sinusoïdales de certaines fréquences $ \ omega $. Bien sûr, il y a des fréquences qui correspondent bien à $ f $ et d'autres qui se rapprochent moins bien. Ainsi, nous avons besoin d'une valeur $ \ hat (\ omega) $ qui nous dit combien d'une oscillation donnée avec une fréquence $ \ omega $ est présent dans l'approximation de $ f $.
Prenons par exemple la fonction rouge d'ici
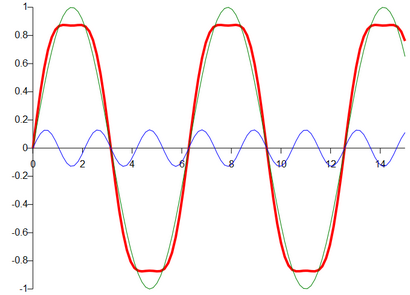
qui est défini comme
L'oscillation verte avec $ \ omega = 1 $ a le plus grand impact sur le résultat, donc disons $$ chapeau \ (1) = 1 $$
L'onde sinusoïdale bleu ($ \ omega = 3 $) a au moins un certain impact, mais il est l'amplitude est beaucoup plus petit. Ainsi nous disons $$ \ hat (3) = 0,13 $$
Maintenant, si nous savions chapeau $ \ (\ omega) $ non seulement pour certains, mais toutes les fréquences possibles $ \ omega $, nous pourrions parfaitement approcher notre fonction $ f $. Et c'est ce que la transformée de Fourier continue fait.
Il faut une certaine fonction $ f (t) $ de temps et retourne une autre fonction $ \ hat (\ omega) = \ mathcal (f) $, sa transformée de Fourier. qui décrit la quantité d'une fréquence donnée est présente dans $ f $. Il est juste une autre représentation de $ f $, de l'information égale, mais avec un tout autre domaine. Souvent, cependant, les problèmes peuvent être résolus beaucoup plus facilement dans cette autre représentation (qui est comme trouver le système de coordonnées approprié).
Mais étant donné une transformée de Fourier, nous pouvons intégrer sur toutes les fréquences, mettre en place les ondes sinusoïdales pondérées et obtenir notre nouveau $ $ f, que nous appelons transformée de Fourier inverse $ \ mathcal ^ $.
Maintenant, pourquoi devrait-on faire cela?
Plus important encore, la transformée de Fourier a de nombreuses propriétés mathématiques belles (à savoir convolution est juste multiplication). Il est souvent beaucoup plus facile de travailler avec les transformées de Fourier qu'avec la fonction elle-même. Donc nous transformer, ont un travail facile avec le filtrage, la transformation et la manipulation des ondes sinus et retransformer après tout.
Disons que nous voulons faire une réduction du bruit sur une image numérique. Plutôt que de manipuler une fonction $ \ text. \ Texte \ à \ texte $, nous transformons la chose et de travailler avec $ \ mathcal (texte \). \ Texte \ à \ texte $. Les parties de haute fréquence qui cause le bruit peut simplement être coupé - $ \ mathcal (texte \) (\ omega) = 0, \ omega>. Hz $. Nous Reprenez et le tour est joué.Exemple 1: multiplication polynomiale
Ceci est l'utilisation de la transformée de Fourier discrète, je suis plus familier. Supposons que vous voulez multiplier deux polynômes de degré n, donnés par leurs coefficients (a0. ..., an) et (b0. ..., bn). Dans leur produit, le coefficient de x k est ck = bk-Σai i. Ceci est une convolution, et de le faire serait prendre naïvement O (n 2) temps.
, Supposons que nous représentons plutôt les polynômes par leurs valeurs aux points 2n. Ensuite, la valeur du polynôme de produit (celui que nous voulons) à tout moment est tout simplement le produit des valeurs de nos deux originaux polynômes. Ainsi, nous avons réduit convolution à la multiplication ponctuelle. La transformée de Fourier et son inverse correspond à une évaluation polynomiale et interpolation, respectivement, pour certains points bien choisis (racines de l'unité). La transformée de Fourier rapide (FFT) est une façon de faire deux dans O (n log n).
Exemple 2: La convolution de distributions de probabilité
Mais au lieu de représenter les variables aléatoires par leur densité, on peut aussi les représenter par leurs fonctions caractéristiques φX (t) = E [e iTX] et φY (t) = E [e Ity]. Ensuite, la fonction caractéristique de X + Y est juste:
φX + Y (t) = E [e it (X + Y)] = φX (t) φY (t) car ils sont indépendants. La fonction caractéristique est la transformée de Fourier en continu la fonction de densité; il est un changement de représentation dans laquelle convolution devient la multiplication ponctuelle.
Pour citer à nouveau la réponse sur MO, de nombreuses transformations que nous voulons étudier (traduction, la différenciation, l'intégration, ...) sont en fait des circonvolutions, de sorte que la transformée de Fourier aide dans un grand nombre de cas.
Pensez à la lumière provenant d'étoiles.
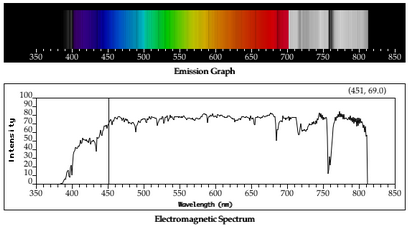
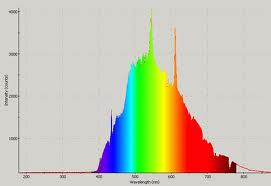
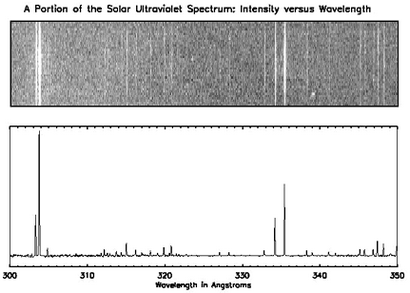
La lumière a une couleur ou un « spectre », mais bien sûr les données proviennent dans un courant de 1-D.
La transformée de Fourier vous donne le spectre de la série chronologique.

(Fourier inverse juste vous ramène du spectre du signal. Alors, qu'est-ce que cela signifie que $ \ mathcal ^ = \ mathcal $?)
Pour entrer dans les mathématiques de celui-ci, rappelez-vous que $ \ cos $ et sont tout simplement déphasés $ sin $ \ versions d'un autre. Mathématiquement, vous additionnez différentes quantités (amplitudes) de différentes $ \ sin ondes $ déphasés et il est un fait surprenant que cela peut ajouter jusqu'à une fonction.
(Comment voulez-vous obtenir une ligne droite comme $ y = x $ par exemple?)
Note: La série transformée ne doit pas être une série chronologique exactement. Vous pouvez paramètrer beaucoup de courbes de $ t $. Par exemple l'écriture ou le contour des empreintes de dinosaures.
Comment est-il utilisé dans l'ingénierie? Traitement du signal, traitement d'image (PDF. Aller à la page 5), et le traitement vidéo utilisent la base de Fourier pour représenter les choses.
Voici ma compréhension de la transformée de Fourier comme il est venu à moi.
Imaginez que vous avez un objet qui fait un son lorsqu'il est secoué (par exemple un verre, diapason, cymbale, corde de guitare, vous le nom). Tout son fait de cette façon est une composition de plusieurs fréquences (il est seulement un hémisphère parfait qui vibre dans une véritable onde harmonique). Je veux maintenant analyser les fréquences présentes dans ce son, et je veux faire de la manière ancienne.
Je mets l'objet quelque part où il est libre d'osciller et faire son. Ensuite, je joue un ton pur dans une certaine fréquence, et mesurer à quel point il se déplace à l'unisson. Si elle se déplace beaucoup à l'unisson, il devrait y avoir beaucoup de cette fréquence dans son son naturel. C'est ce que la transformée de Fourier ne, que des fonctions.
D'une manière générale, la transformée de Fourier d'une fonction $ f $ est défini par $$ chapeau \ f (\ omega) = \ int _ ^ \ infty f (z) e ^ dz $$ Le terme exponentiel est un mouvement de cercle dans le plan complexe avec une fréquence $ \ omega $. Il joue le rôle du ton pur que nous avons joué à l'objet. La raison pour laquelle nous utilisons un terme exponentiel complexe au lieu d'un terme pur trigonométrique est que, avec un terme de $ péché $ \ nous pourrions être malchanceux avec la phase. De cette façon, nous obtenons un résultat avec la même valeur absolue, peu importe la phase, seule la direction de $ \ elon (\ omega) $ variera.
Si $ f $ a beaucoup de $ \ oscillation oméga -Fréquence de $ en elle, le nombre $ f (z) e ^ $ aura tendance à aligner dans la même direction générale dans le plan complexe pour différents $ z $ (exactement quelle direction qui dépend de la phase, comme il est indiqué ci-dessus). Comme vous intégrez plus de $ z $, $ \ elon (\ omega) $ devient relativement importante.
D'autre part, si $ f $ n'a pas beaucoup $ \ oscillation oméga -Fréquence de $ en elle, le integrand finira sur tous les côtés de l'origine pour différents $ z $ et que vous intégrez, le résultat $ \ hat f (\ omega) $ sera faible.
Je pense que les idées sont plus claires dans le cas de la transformée de Fourier discrète, qui peut être très bien compris avec rien, mais l'algèbre linéaire de dimension finie.
Parce que les opérateurs de décalage invariant sont très importants dans le traitement et l'analyse numérique le signal, nous aimerions les comprendre aussi bien que possible. Et l'une des meilleures façons de comprendre un opérateur linéaire est de trouver une base de vecteurs propres pour elle. En algèbre linéaire, il existe plusieurs théorèmes « de diagonalisation simultanée » qui stipulent que, sous certaines hypothèses, les opérateurs linéaires qui commutent peuvent être simultanément diagonalise. Cela suggère une stratégie pour diagonalisation un opérateur linéaire décalage invariant $ A $. Parce que $ A $ avec $ S permute $, nous pouvons d'abord trouver une base de vecteurs propres pour $ S $. , Nous pouvons (nous l'espérons) invoquer un théorème de diagonalisation simultanée pour montrer que cette base de vecteurs propres pour $ S $ est également une base de vecteurs propres pour $ A $.
Notez que $ S $ préserve les normes, il est donc unitaire. Chaque opérateur unitaire est normal. Ainsi, le théorème spectral garantit que $ S $ a une base orthonormée de vecteurs propres. De plus, vous pouvez facilement trouver les vecteurs propres de $ S $ à la main en ce moment. Après une courte (et amusant) le calcul, vous découvrirez que si $ \ omega $ est un $ N $ e racine de l'unité alors le vecteur $$ v_ \ omega = \ begin 1 \\ \ omega \\ \ omega ^ 2 \ \ \ vdots \\ \ omega ^ \ end $$ est un vecteur propre de $ S $. Et quelle est la valeur propre? Allez-y et passez v_ $ \ omega $ en ce moment, et vous verrez immédiatement la valeur propre. Il est $ \ omega $, non? C'était amusant!
Parce qu'il ya N $ N $ $ $ distincte e racines de l'unité, nous avons trouvé $ N $ et des valeurs propres distinctes vecteurs propres correspondants pour $ S $. En fait, il y a un théorème de diagonalisation simultanée qui dit que parce que les valeurs propres de $ S $ sont distincts, tout opérateur linéaire $ A $ qui commute avec $ S $ est diagonalise par les mêmes vecteurs propres.
Nous avons maintenant découvert comment diagonaliser tout opérateur linéaire décalage invariant. La base de vecteurs propres que nous avons découvert est appelé la « base de Fourier discrète ». La « transformation de Fourier discrète » est simplement la transformation linéaire qui change de base à partir de la base standard de la base de Fourier discrète.
Une réponse plus compliquée (mais il va être imprécise, parce que je ne l'ai pas touché ce depuis 15 ans.) Est le suivant.
Dans un espace 3-dimentionnelle (par exemple) on peut représenter un vecteur v par ses coordonnées de points d'extrémité, x, y, z, d'une manière très simple. Vous choisissez trois vecteurs qui sont d'une longueur unitaire et orthogonale les uns aux autres (une base), dis-je. j et k. et calculer les coordonnées en tant que tels:
Dans l'espace multidimentionnelle, les équations tiennent toujours. Dans un espace infini discret, les coordonnées et les vecteurs de base deviennent une séquence. Le produit scalaire devient une somme infinie.
Dans un espace infini en continu (comme l'espace de bonnes fonctions) les coordonnées et les bases deviennent des fonctions et le produit scalaire d'une infinie intégrale.
Maintenant, la transformée de Fourier est exactement ce genre d'opération (basé sur un ensemble de fonctions de base qui sont essentiellement un ensemble de Sines et cosinus). En d'autres termes, il est une représentation différente de la même fonction par rapport à un ensemble particulier de fonctions de base.
En conséquence, par exemple, des fonctions du temps, représentées contre des fonctions du temps et de l'espace (en d'autres termes intégrés au fil du temps, multiplié par les fonctions de l'espace et le temps), deviennent des fonctions de l'espace, et ainsi de suite.